Are you using a false IRR generated from Excel or handheld financial calculator?

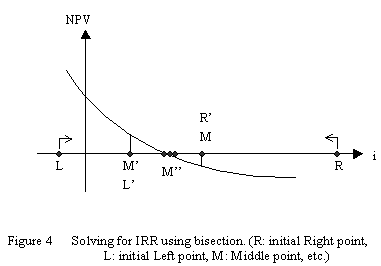
IRR, the Internal Rate of Return, is defined as the discount rate that generates a zero net present value. So mathematically, IRRs are just the roots of a NPV function. Sometimes there are multiple roots for a NPV function. In Excel, you need to provide a 'guess' value so that the IRR function can return you with a value closest to the guess value. But how do you know which one is the real IRR?

Here is an example. Assume we have a series of cash flows: -10, 150, -145, 80, -250. You may use Excel to calculate IRR. There are two roots: 50.12% and 1299.57%. Each one generates zero NPV. Which root then is the real IRR?

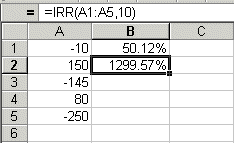
Two IRRs from Excel's IRR function. Both are false.

[Answer]
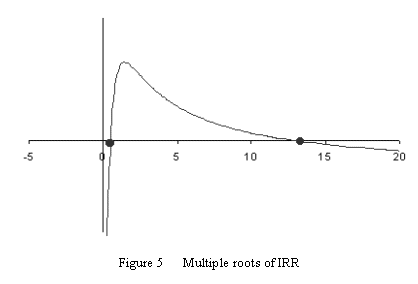
The answer is that neither is a meaningful IRR. Let's look at the cash flows first. With a discount rate of zero, this project's net present value is negative. It is impossible to lose money and still have a positive rate of return. The equation is plotted on the coordinate plane in Figure 5. The curve intercepts the x-axis at 50.12% and 1299.57%. The point 1299.57% is outside of the meaningful IRR range and should be discarded. The NPV at point 50.12% has a positive, increasing slope, which contradicts the concept of 'discounting'. So, it is not a meaningful IRR either. Precision finds the IRR based on bisection method and function checking, therefore, for this series of cash flows, Precision returns 'N/A' - not available.

We have more examples and discussions in our user's manual. Some false IRRs look like they are 'real'. Precision's IRR function first checks NPV then the slope of the function. It will return you with meaningful IRRs not mathematical roots. If you use IRR in your project evaluation, you should be very careful about this. Let Precision give you peace of mind using IRRs.

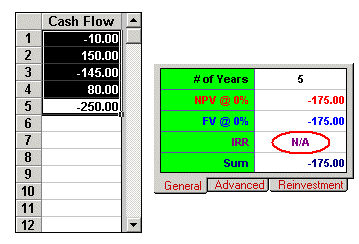
IRR from Precision Financial Calculator